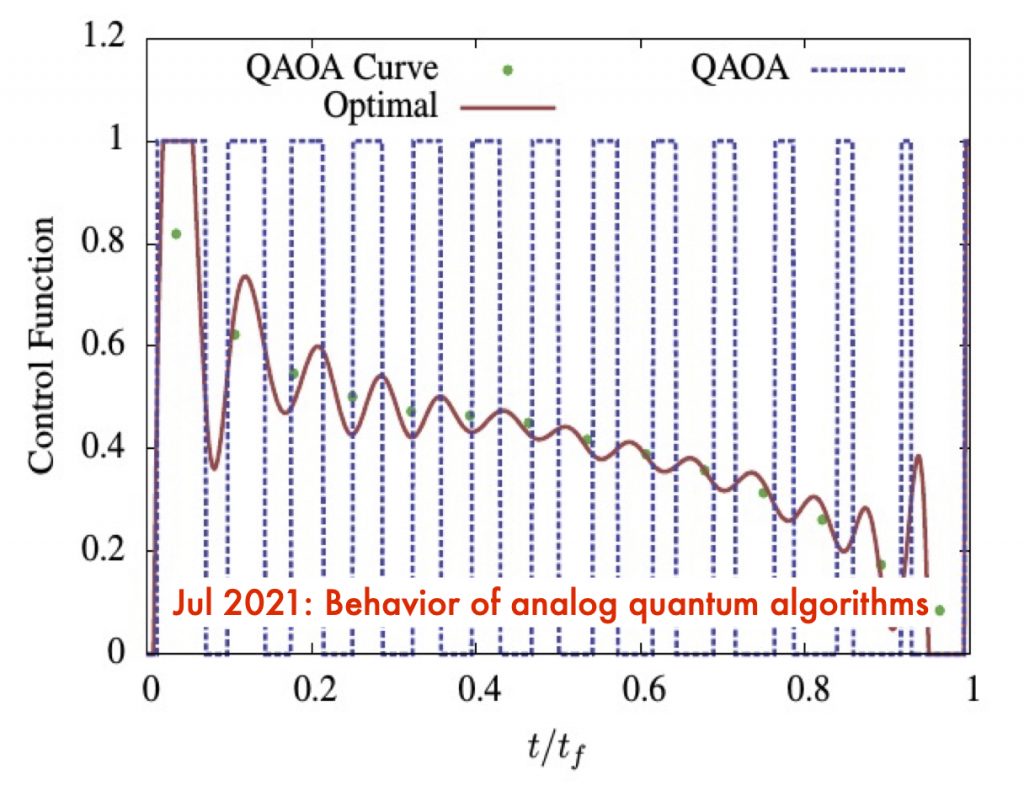
We show a relationship between quantum annealing (QA) in the near-adiabatic regime and optimal quantum approximate optimization algorithm (QAOA) parameters that establishes when the QAOA becomes an approximation to QA.
The relationship establishes a “universal” curve that the p QAOA parameters approach as p goes to infinity. This implies a starting value for a QAOA optimization with p parameters based on a linear interpolation of the optimal values found for q<p that is demonstrably more efficient than competing methods.
We explore how the optimal QAOA procedure, through a product formula expansion, approaches a smooth adiabatic procedure but with superposed oscillatory pattern that can be be explained in terms of the interactions between the grounds state and first excited state that effect coherent error cancellation of diabatic transitions (i.e. a counter-diabatic term).
For details see
“Behavior of Analog Quantum Algorithms”, Lucas T. Brady, Lucas Kocia, Przemyslaw Bienias, Aniruddha Bapat, Yaroslav Kharkov, Alexey V. Gorshkov arXiv:2107.01218.