Uncategorized

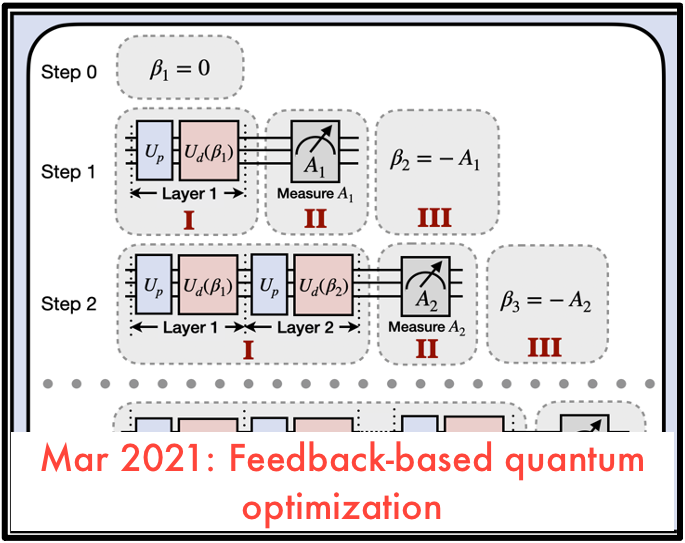
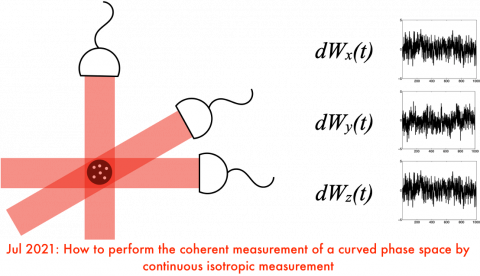
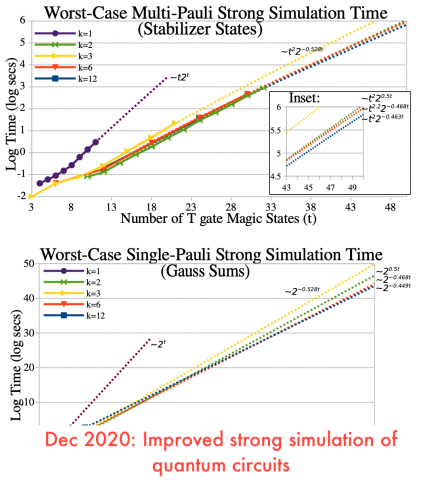
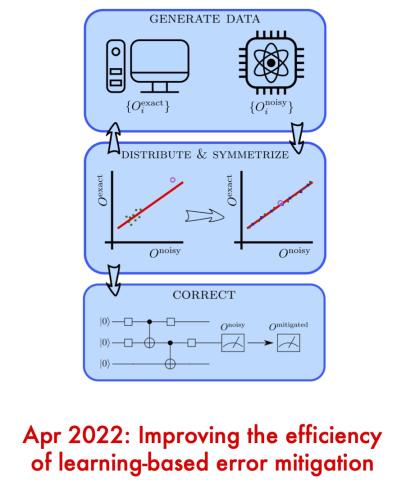
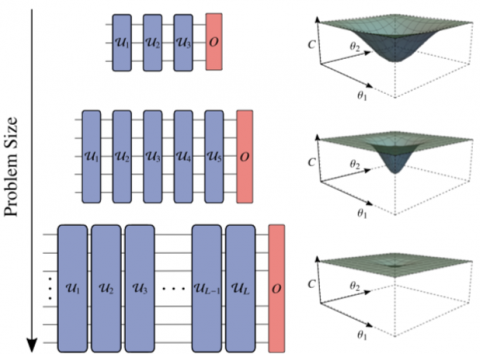
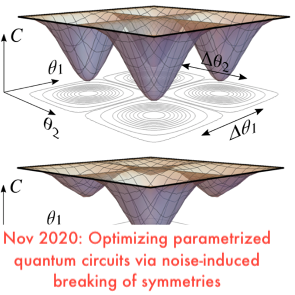
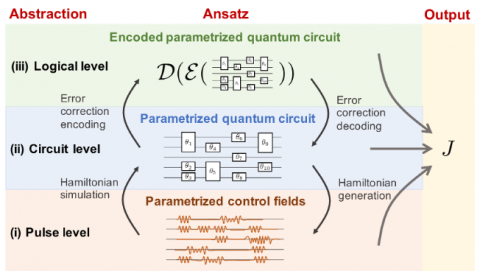
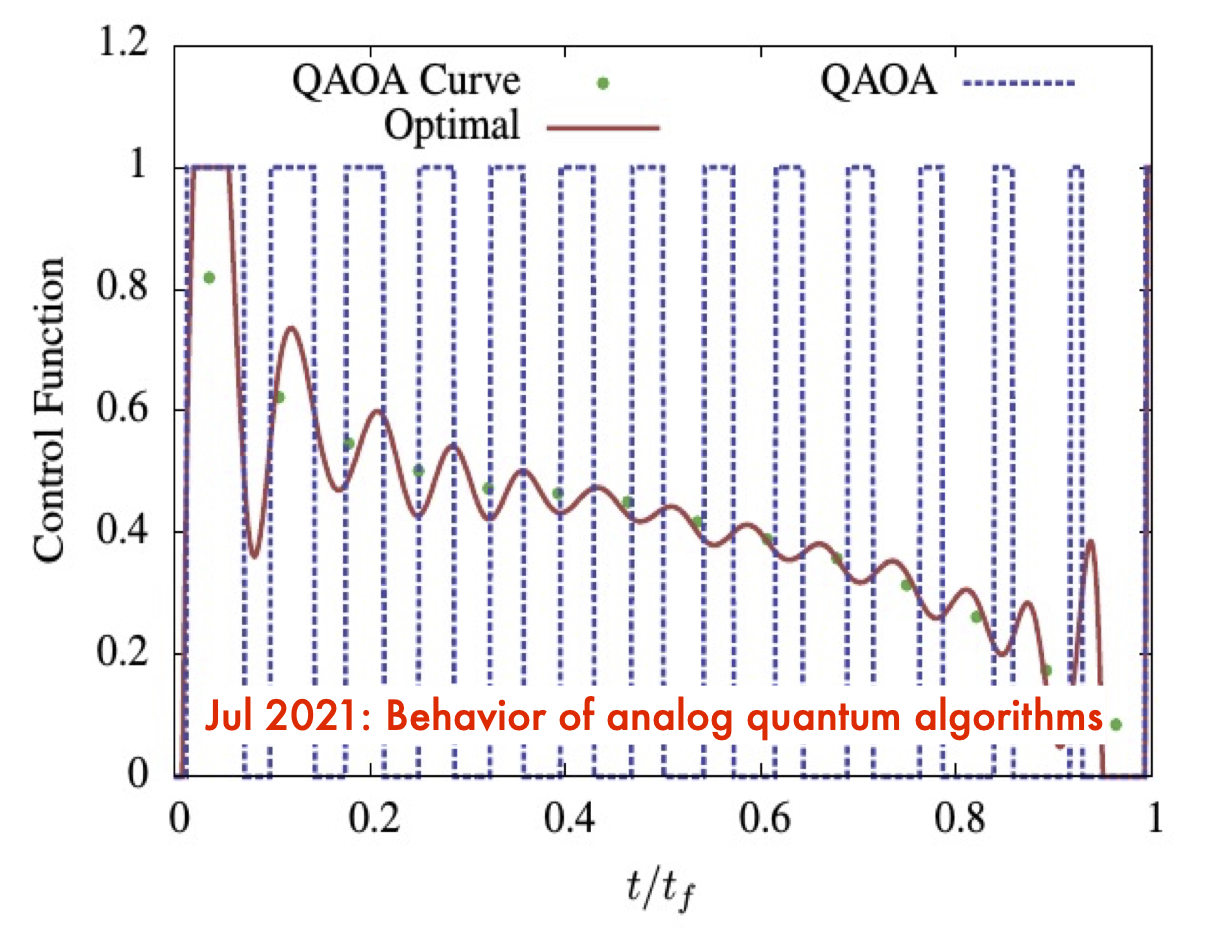
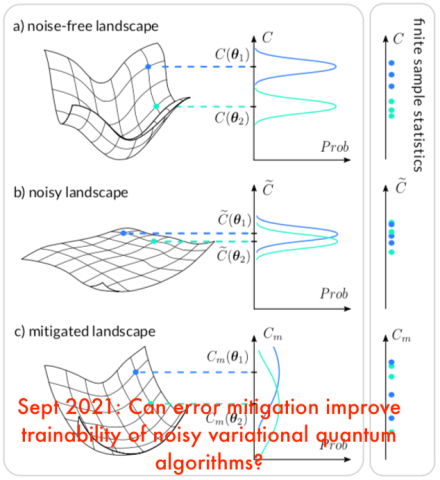
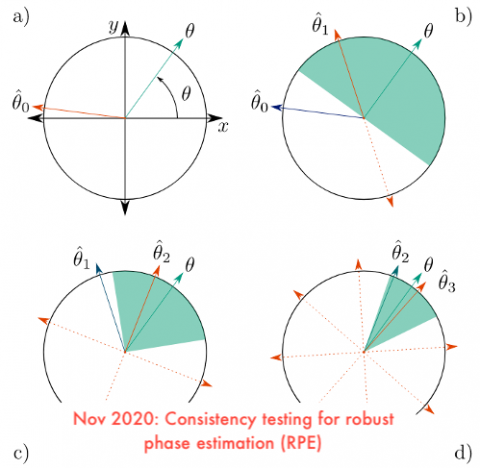
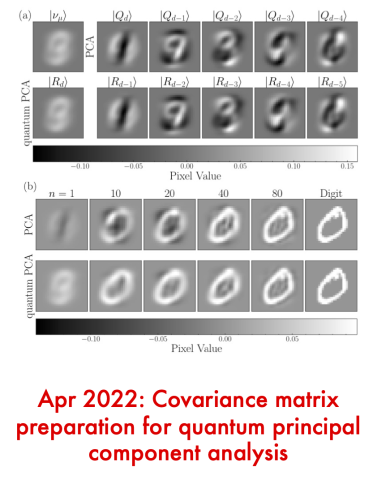
Post, September 19, 2020 • We provide an overview of variational quantum algorithms (VQAs) from the perspective of quantum optimal control (QOC). We integrate both fields in a common framework that enables identification of several QOC-inspired avenues for improving VQA performance on near-term quantum hardware. VQAs present some of the most promising applications of near-term...

Post, August 30, 2021 • We show a relationship between quantum annealing (QA) in the near-adiabatic regime and optimal quantum approximate optimization algorithm (QAOA) parameters that establishes when the QAOA becomes an approximation to QA. The relationship establishes a “universal” curve that the p QAOA parameters approach as p goes to infinity. This implies a...

Post, July 22, 2022 • Variational quantum algorithms (VQAs) may be the best hope for near-term quantum advantage, but noise significantly affects their performance. We study whether error mitigation can improve the trainability of VQAs. We find that error mitigation cannot solve the exponential scaling associated with noise-induced barren plateaus, but it can improve trainability...

Post, February 25, 2021 • The robustness of robust phase estimation (RPE) relies on noise being below a particular threshold. While it is difficult or impossible to directly test the violation of this threshold, we developed a set of consistency checks that herald whether there might be violations in a data set. We tested these checks for...

Post, July 22, 2022 • It was recently shown that quantum PCA can provide an exponential speedup over classical methods for PCA. However, no method to prepare the covariance matrix on a quantum device was known. We fill this gap with a simple approach, unlocking the possibility of near-term quantum PCA. We find a simple,...

Post, October 28, 2020 • We present a fully customizable construction for designing quantum codes for systems of fermions on a quantum computer. The required number of qubits and the gate counts determine the feasibility of a quantum simulation experiment. The construction presented lets one realize a trade-off between these two resources and in some cases lower...

Post, November 16, 2020 • "A quantum bridge". Article in DEIXIS by Monte Bagsall on Department of Energy sponsored quantum information science research at Sandia, including a discussion of OVER-QC. Figure shows Sandia's HOA 2 ion trap and is courtesy Susan Clark and the trapped ions group at Sandia.

Post, October 17, 2022 • Preparation of many-body states is an important task for applications such as quantum simulation and quantum sensing, and digitized adiabatic evolution (DAE) is the most common and practical way to achieve this task on a quantum computer. We derive and numerically demonstrate improved error bounds for state preparation via DAE....

Post, July 6, 2020 • We introduce a hybrid quantum algorithm for the problem of designing shaped electromagnetic fields to optimally control molecular systems. The algorithm could be used on future quantum computers to design optimal fields for coherently controlling molecular transformations relevant to chemical, biological, and materials applications.  For details see "Digital quantum simulation...

Post, July 22, 2022 • Dynamical simulation and QML are both promising fields, and our work is the first to explore their intersection. We show that QML generalization bounds can guarantee good performance of certain dynamical simulation algorithms with minimal training data required. In the process, we develop a new simulation algorithm that is promising....

Post, April 22, 2021 • We have shown the electronic structure problem is QMA-hard without magnetic field but restricted to a fixed orbital basis. Our main result shows consider electronic structure Hamiltonians restricted to a fixed number of electrons and projected into a fixed single-particle basis. We conclusively demonstrate that these properties do not add...

Post, July 6, 2020 • We propose a novel, scalable error mitigation method that applies to gate-based quantum computers.  The method uses training data from quantum circuits that are classically efficiently simulatable to generate fitting models that can be used to correct for the effects of noise on the output of classically intractable quantum circuits. For...

Post, July 22, 2022 • Real-world quantum computations need to be verified to rule out errors.  But most useful computations cannot be efficiently verified by classical simulations. Our method enables verification, by efficiently quantifying how accurately a given computer can implement a given algorithm’s quantum circuits. We introduced a simple and efficient technique for measuring...

Post, August 8, 2020 • We extended robust phase estimation (RPE) – a protocol for characterizing single-qubit gates – to the evaluation of energy differences in quantum simulation. We demonstrated our protocol on IBM’s Quantum Experience, verifying that it achieves optimal Heisenberg-like scaling. We also proved that our approach has a relatively high tolerance for...

Post, July 6, 2020 • We find non-trivial upper bounds to the cost of strong simulation of quantum circuits using T-gate magic states (a common method for classically simulating quantum circuits). We break through a long-standing barrier that has been hindering the quantum information community from answering a fundamental open problem of broad interest: how slowly can...

Post, April 23, 2021 • We introduce a constructive protocol that uses feedback from qubit measurements to solve discrete optimization problems on quantum computers. The use of feedback removes the need for any classical optimization effort. The protocol could be used on quantum computers to solve discrete optimization problems with a range of applications spanning...

Post, August 30, 2021 • Originally introduced in 1960 by John Klauder, the spin-coherent measurement is the heart of generalized quantization.  Since 2001, it was understood that the spin-coherent measurement could somehow be done in a way analogous to how Arthurs & Kelly anticipated quantum heterodyne for the standard coherent measurement of optics.  However, physicists...

Post, February 25, 2021 • Multi-Pauli measurements on magic states is one way to formulate universal quantum computing. We lower the asymptotic bound to 2∼0.463t for multi-Pauli measurements on t magic states, improving over the best previously found bound of 2∼0.468t. This not only improves our understanding of the difficulty of classically simulating quantum circuits, but...

Post, July 22, 2022 • Error mitigation will play an important role in practical applications of near-term noisy quantum computers. Current error mitigation methods typically concentrate on correction quality at the expense of frugality (as measured by the number of additional calls to quantum hardware). To fill the need for highly accurate, yet inexpensive techniques,...

Post, August 8, 2020 • We highlight obstructions to using quantum approaches as a replacement for standard self-consistent field method solutions using simple, well-motivated examples of convergence issues. Due to multiple local minima there is no a priori guarantee that typical quantum approaches will find the global solution. We conclude that the application of quantum...

Post, August 30, 2021 • We present Lyapunov control-inspired protocols to solve combinatorial optimization problems on quantum computers. Our control-inspired protocols do not require any classical optimization effort. They could be used on quantum computers to solve discrete optimization problems with a range of applications spanning supply chain and logistics. This is a companion paper...

Post, October 17, 2022 • Machine learning can help make better approximation to Kohn-Sham potential. In this work, we present the first demonstration of using machine learning to investigate Kohn-Sham potential from the evolution of system’s density without resorting to the exact Kohn-Sham potential. Hamilton’s equations in Kohn-Sham system was developed under adiabatic approximation. Based...

Post, July 6, 2020 • Noise mitigation and reduction will be crucial for obtaining useful answers from near-term quantum computers. We present a general framework based on machine learning for reducing the impact of quantum hardware noise and limitations on quantum circuits. Given a computational task and a device model, our noise-aware circuit learning algorithm...

Post, August 8, 2020 • We rigorously prove a serious limitation for Variational Quantum Algorithms (VQAs), in that the noise causes the training landscape to have a barren plateau (i.e., vanishing gradient). For local Pauli noise, we prove that the gradient vanishes exponentially in the number of layers L. This implies exponential decay in the...

Post, February 25, 2021 • We analytical prove two results for parametrized quantum circuits (PQCs): (1) We find an exponentially large symmetry, which leads to an exponentially large degeneracy in the cost landscape minima. (2) We show that this degeneracy is broken by noise. We propose a novel optimizer called Symmetry-based minima hopping (SYMH), that...