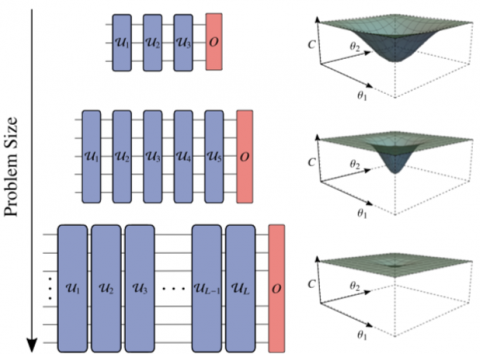
We rigorously prove a serious limitation for Variational Quantum Algorithms (VQAs), in that the noise causes the training landscape to have a barren plateau (i.e., vanishing gradient). For local Pauli noise, we prove that the gradient vanishes exponentially in the number of layers L. This implies exponential decay in the number of qubits n when L scales as a sufficiently large polynomial in n.
This new limitation we identify will adversely impact applications such as optimization and chemistry on near-term quantum computers.
For details see “Noise-Induced Barren Plateaus in Variational Quantum Algorithms”, by Samson Wang, Enrico Fontana, M. Cerezo, Kunal Sharma, Akira Sone, Lukasz Cincio, Patrick J. Coles. arXiv:2007.14384.