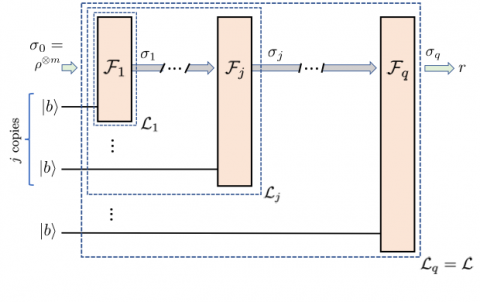
We analyze the complexity of quantum state verification (QSV) in the context of solving systems of linear equations and provide complexity bounds that show that any verification procedure for this problem is “expensive”.
Our results are an important contribution to quantum complexity and, among other implications, show that checking that the solution to a linear system is correct can be prohibitively expensive for near-term quantum devices. Our proof techniques can be generalized and applied to related state-verification problems.