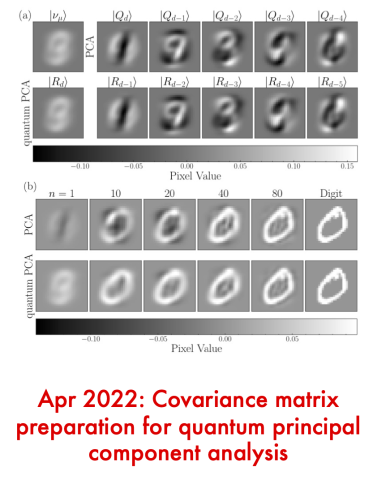
It was recently shown that quantum PCA can provide an exponential speedup over classical methods for PCA. However, no method to prepare the covariance matrix on a quantum device was known. We fill this gap with a simple approach, unlocking the possibility of near-term quantum PCA.
We find a simple, near-term method for preparing an approximation of the covariance matrix on a quantum computer, allowing for quantum principal component analysis (quantum PCA). For quantum data, our method is exact (no approximation). For classical data, our method is PCA without centering, and we provide rigorous bounds on the accuracy.
Our main results are theorems proving that the ensemble average density matrix for a given dataset is either equal to the covariance matrix (for quantum data) or a close approximation of it (for classical data). We also illustrate this with numerics (see right panel).
For details see
“Covariance matrix preparation for quantum principal component analysis”, M. Hunter Gordon, M. Cerezo, L. Cincio, P.J. Coles. arXiv:2204.03495.