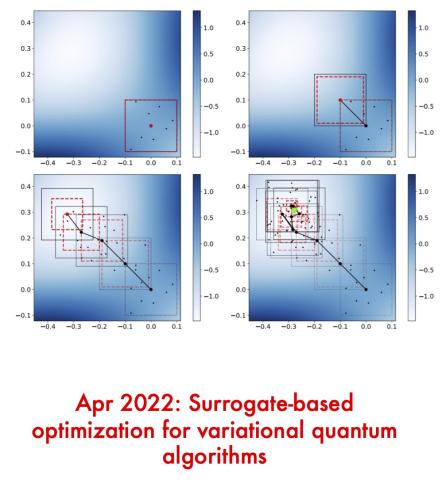
The most useful potential applications of quantum computers will require programs containing millions of operations, but current state-of-the-art devices are able to run programs that are only a small fraction of that length. To accommodate this limitation, procedures known as “variational quantum algorithms” (VQAs) have been developed, which attempt to find the optimal parameters for a particular problem by running many repetitions of a relatively short quantum program, combined with a classical optimization technique which adjusts the parameters for each repetition. In our work, we develop and demonstrate a new classical optimization technique that outperforms the most commonly-used techniques, which will reduce the runtime and increase the reliability of VQAs on these near-term devices.
The classical optimization piece of VQAs requires obtaining measurement results from the quantum program for many different parameter settings. But due to the probabilistic nature of quantum measurement, the results from the quantum program are fundamentally noisy, which poses a problem for classical optimization techniques that rely on the smoothness of the underlying landscape. Our technique works by converting the noisy measurement data into a smooth “surrogate” representation of the underlying landscape, which allows efficient use of classical optimizers. We demonstrate our technique on several instances of common VQAs and show that it can achieve significantly better results than existing techniques using an equivalent number of repetitions of the quantum program.
Based on these results, we believe that this technique is broadly applicable to the use of VQAs on near-term quantum computers. In addition, investigating alternative methods for constructing the surrogate representation of the underlying landscape is a promising avenue for future research in this area.
For details see
“Surrogate-based optimization for variational quantum algorithms”, Ryan Shaffer, Lucas Kocia, Mohan Sarovar. arXiv:2204.05451.