-
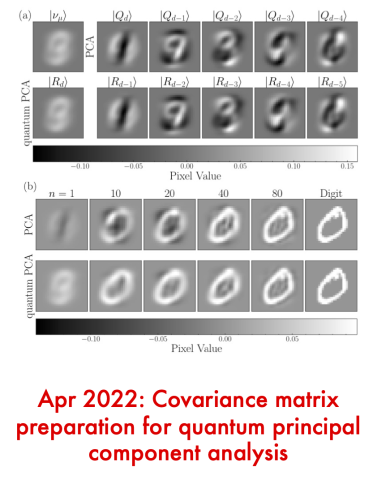
Covariance matrix preparation for quantum principal component analysis
It was recently shown that quantum PCA can provide an exponential speedup over classical methods for PCA. However, no method to prepare the covariance matrix on a quantum device was known. We fill this gap with a simple approach, unlocking the possibility of near-term quantum PCA. We find a simple, near-term method for preparing an…
-
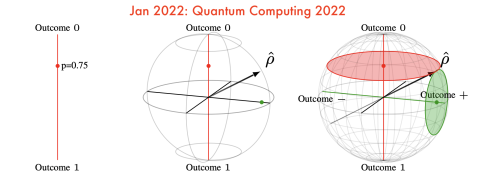
Quantum Computing 2022
We provide a tour of quantum computing and quantum technology that is aimed to be comprehensible to scientists and engineers without becoming a popular account. There is high need for sober assessments of quantum of the promise of quantum technology appropriate for the quantum interested. We have aimed to cite the most recent topical reviews,…
-
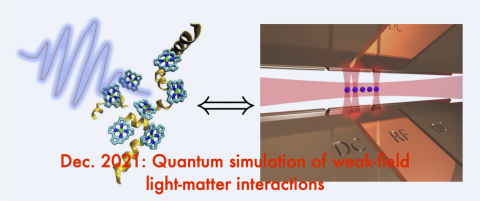
Quantum simulation of weak-field light-matter interactions
We develop a quantum simulation approach that enable platforms with controllable bosonic degrees of freedom, such as the trapped ions and circuit-QED, to simulate the dynamics of matter in response to illumination by extremely weak light fields. The dynamics of matter under weak-field illumination dictates the behavior of photodetectors, photovoltaics, and biochemical systems such as…
-
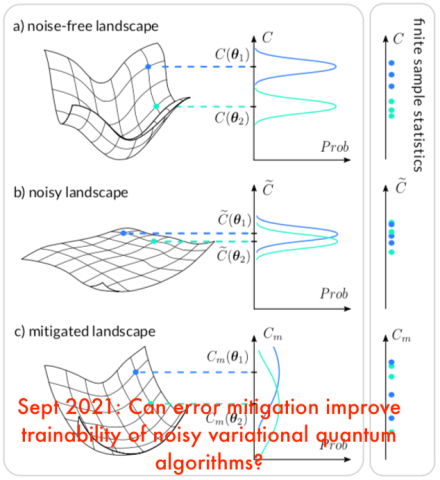
Can error mitigation improve trainability of noisy variational quantum algorithms?
Variational quantum algorithms (VQAs) may be the best hope for near-term quantum advantage, but noise significantly affects their performance. We study whether error mitigation can improve the trainability of VQAs. We find that error mitigation cannot solve the exponential scaling associated with noise-induced barren plateaus, but it can improve trainability in some cases. Our work…
-
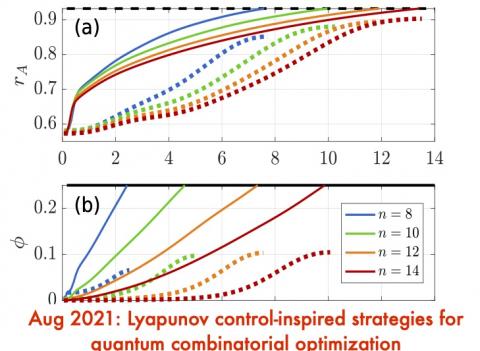
Lyapunov control-inspired strategies for quantum combinatorial optimization
We present Lyapunov control-inspired protocols to solve combinatorial optimization problems on quantum computers. Our control-inspired protocols do not require any classical optimization effort. They could be used on quantum computers to solve discrete optimization problems with a range of applications spanning supply chain and logistics. This is a companion paper to “Feedback-based quantum optimization” [arXiv:2103.08619] and presents…
-
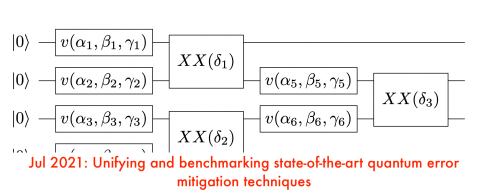
Unifying and benchmarking state-of-the-art quantum error mitigation techniques
Error mitigation is an essential component of achieving practical quantum advantage in the near term, and a number of different approaches have been proposed. In this work we unify three recently proposed error mitigation methods: zero-noise extrapolation (ZNE), Clifford-data regression (CDR), and virtual distillation (VD). We unify these three methods under a general data-driven error mitigation framework…
-
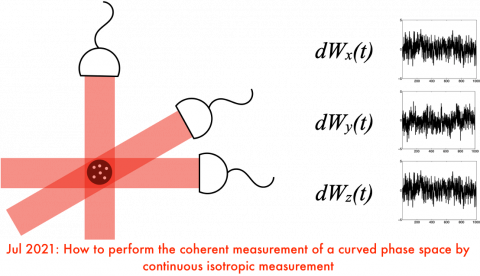
How to perform the coherent measurement of a curved phase space by continuous isotropic measurement
Originally introduced in 1960 by John Klauder, the spin-coherent measurement is the heart of generalized quantization. Since 2001, it was understood that the spin-coherent measurement could somehow be done in a way analogous to how Arthurs & Kelly anticipated quantum heterodyne for the standard coherent measurement of optics. However, physicists were missing the mathematical concepts…