-
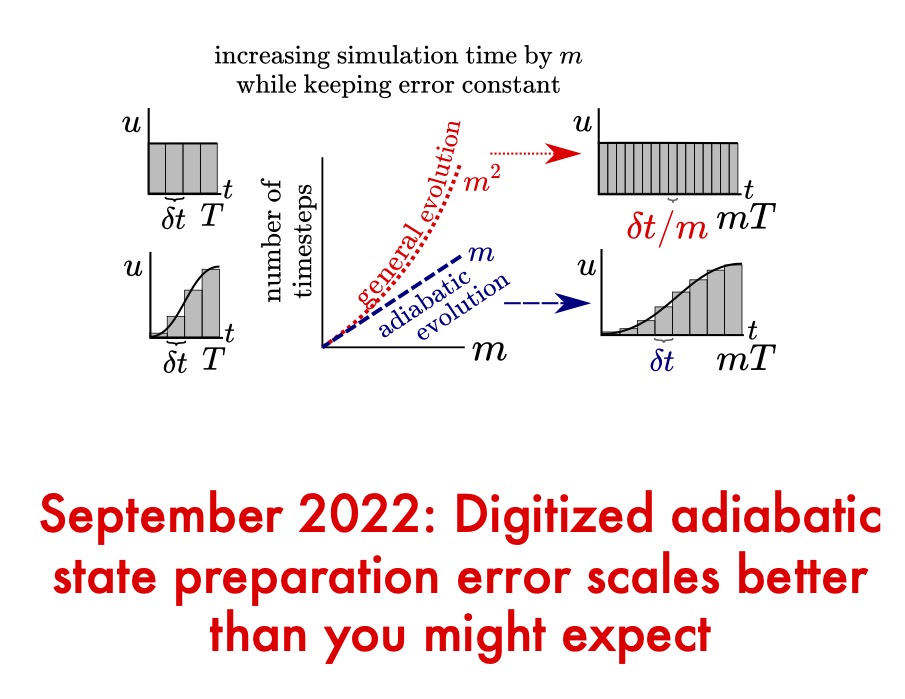
Digital adiabatic state preparation error scales better than you might expect
Preparation of many-body states is an important task for applications such as quantum simulation and quantum sensing, and digitized adiabatic evolution (DAE) is the most common and practical way to achieve this task on a quantum computer. We derive and numerically demonstrate improved error bounds for state preparation via DAE. These new bounds explain several…
-
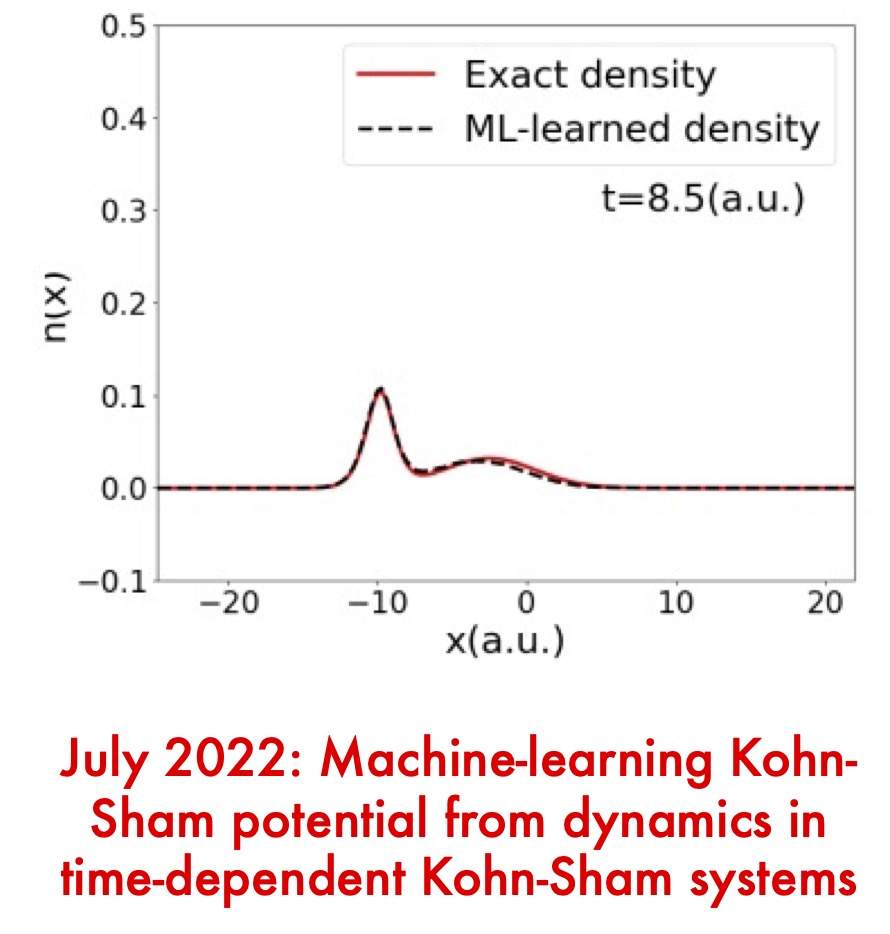
Machine-learning Kohn-Sham potential from dynamics in time-dependent Kohn-Sham systems
Machine learning can help make better approximation to Kohn-Sham potential. In this work, we present the first demonstration of using machine learning to investigate Kohn-Sham potential from the evolution of system’s density without resorting to the exact Kohn-Sham potential. Hamilton’s equations in Kohn-Sham system was developed under adiabatic approximation. Based on the equations, a neural…
-
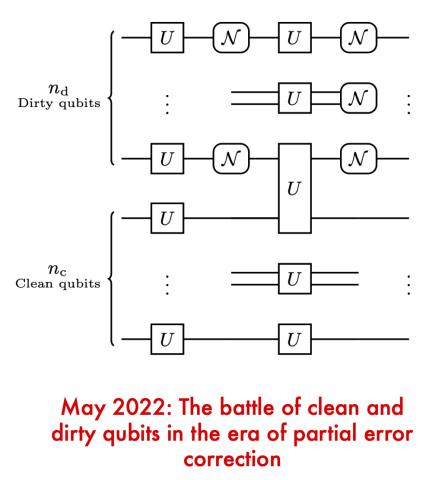
The battle of clean and dirty qubits in the era of partial error correction
When error correction becomes possible it will be necessary to dedicate a large number of physical qubits to each logical qubit. Error correction allows for deeper circuits to be run, but each additional physical qubit can potentially contribute an exponential increase in computational space, so there is a trade-off between using qubits for error correction…
-
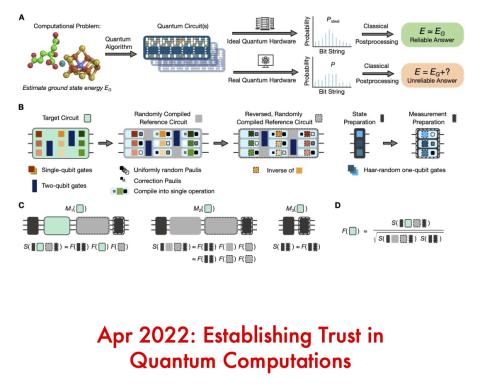
Establishing trust in quantum computations
Real-world quantum computations need to be verified to rule out errors. But most useful computations cannot be efficiently verified by classical simulations. Our method enables verification, by efficiently quantifying how accurately a given computer can implement a given algorithm’s quantum circuits. We introduced a simple and efficient technique for measuring the fidelity with which an…
-
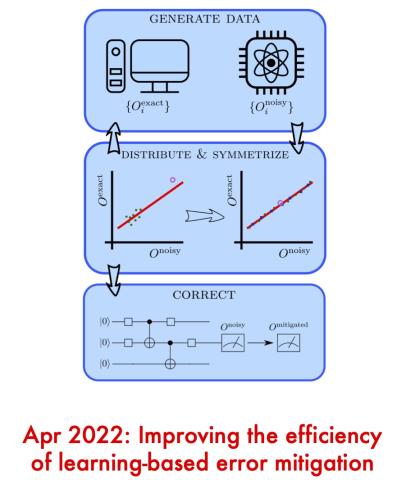
Improving the efficiency of learning-based error mitigation
Error mitigation will play an important role in practical applications of near-term noisy quantum computers. Current error mitigation methods typically concentrate on correction quality at the expense of frugality (as measured by the number of additional calls to quantum hardware). To fill the need for highly accurate, yet inexpensive techniques, we introduce an error mitigation…
-
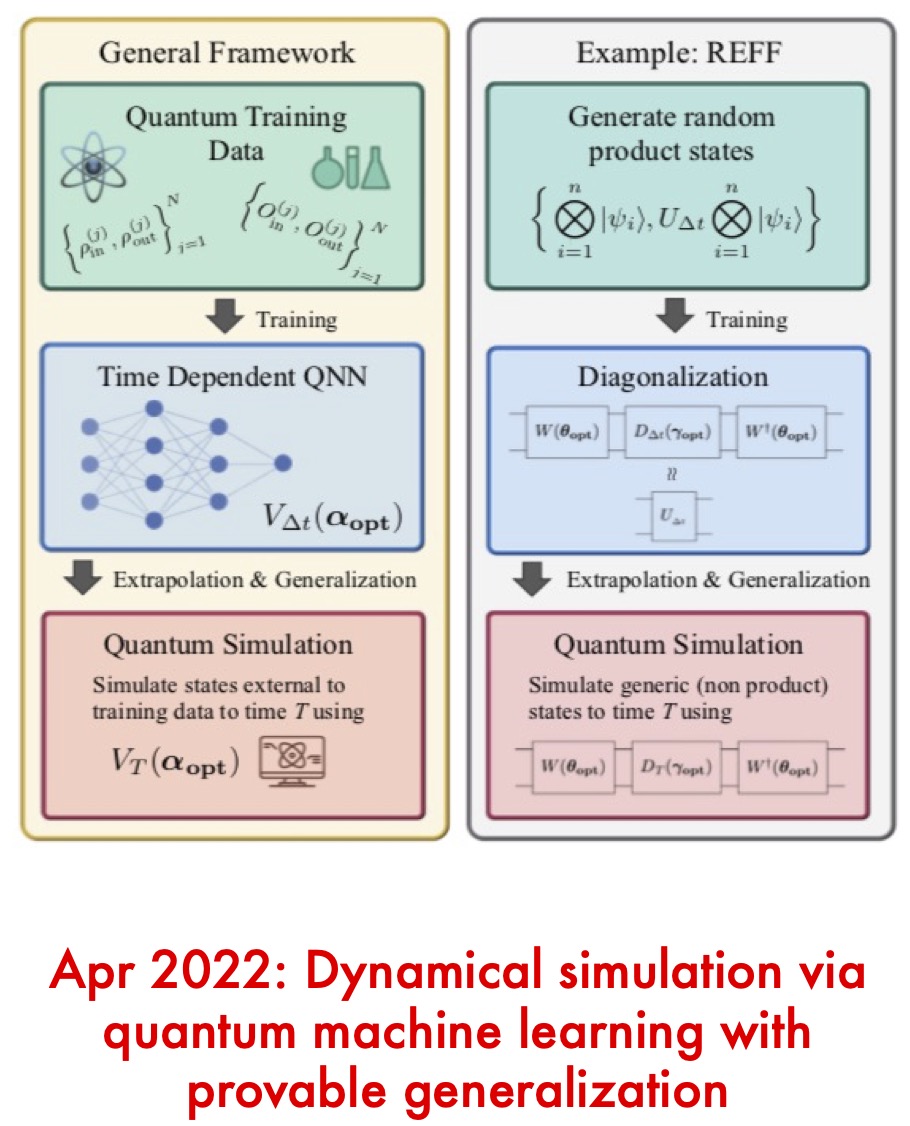
Dynamical simulation via quantum machine learning with provable generalization
Dynamical simulation and QML are both promising fields, and our work is the first to explore their intersection. We show that QML generalization bounds can guarantee good performance of certain dynamical simulation algorithms with minimal training data required. In the process, we develop a new simulation algorithm that is promising. We unify dynamical simulation and…
-
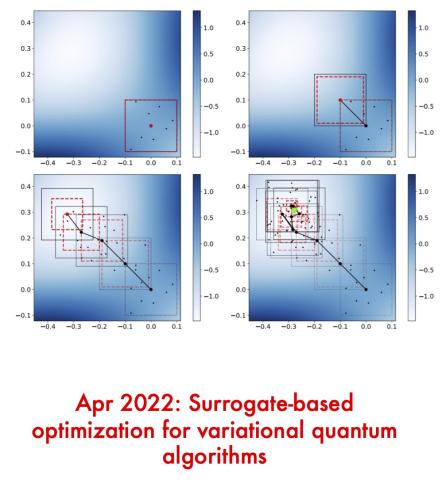
Surrogate-based optimization for variational quantum algorithms
The most useful potential applications of quantum computers will require programs containing millions of operations, but current state-of-the-art devices are able to run programs that are only a small fraction of that length. To accommodate this limitation, procedures known as “variational quantum algorithms” (VQAs) have been developed, which attempt to find the optimal parameters for…