-
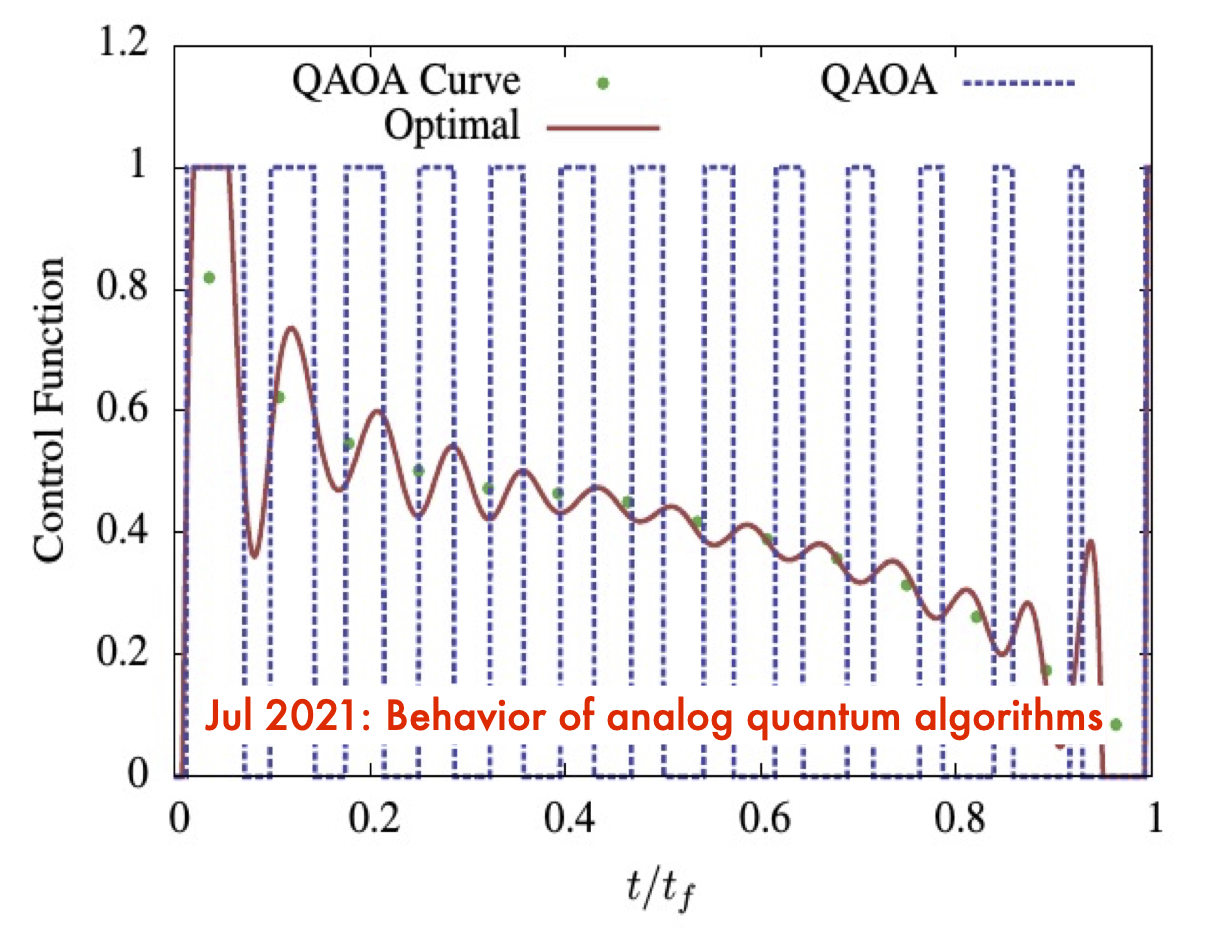
Behavior of Analog Quantum Algorithms
We show a relationship between quantum annealing (QA) in the near-adiabatic regime and optimal quantum approximate optimization algorithm (QAOA) parameters that establishes when the QAOA becomes an approximation to QA. The relationship establishes a “universal” curve that the p QAOA parameters approach as p goes to infinity. This implies a starting value for a QAOA…
-
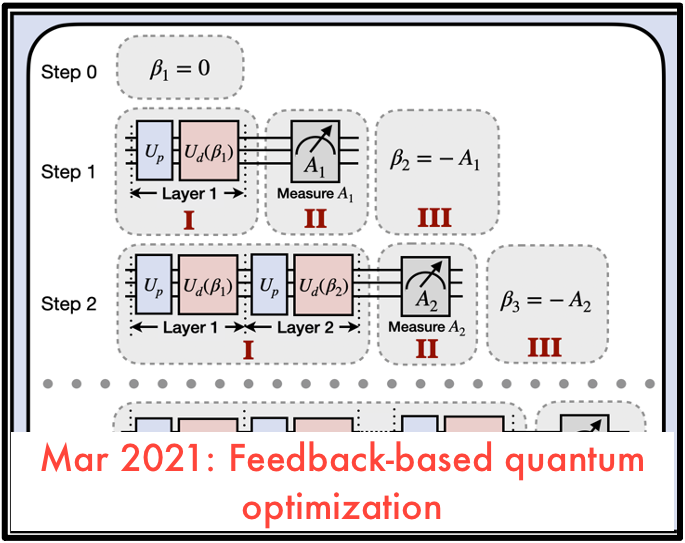
Feedback-based quantum optimization
We introduce a constructive protocol that uses feedback from qubit measurements to solve discrete optimization problems on quantum computers. The use of feedback removes the need for any classical optimization effort. The protocol could be used on quantum computers to solve discrete optimization problems with a range of applications spanning supply chain and logistics. We…
-
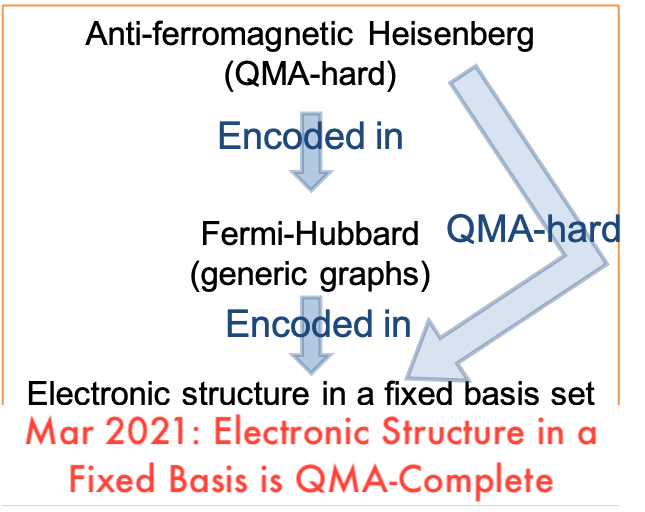
Electronic Structure in a Fixed Basis is QMA-complete
We have shown the electronic structure problem is QMA-hard without magnetic field but restricted to a fixed orbital basis. Our main result shows consider electronic structure Hamiltonians restricted to a fixed number of electrons and projected into a fixed single-particle basis. We conclusively demonstrate that these properties do not add enough structure to enable the…
-
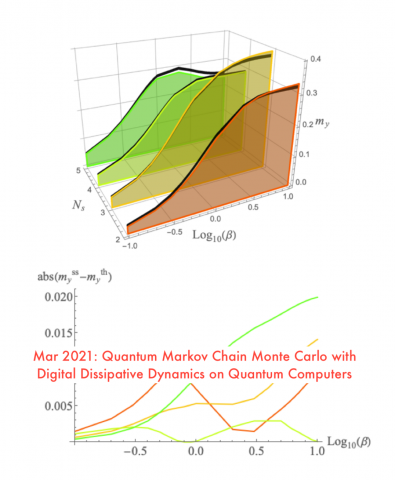
Quantum Markov Chain Monte Carlo with Digital Dissipative Dynamics on Quantum Computers
We develop a digital quantum algorithm that simulates interaction with an environment using a small number of ancilla qubits. By combining periodic modulation of the ancilla energies, or spectral combing, with periodic reset operations, we are able to mimic interaction with a large environment and generate thermal states of interacting many-body systems. Modeling the dynamics…
-
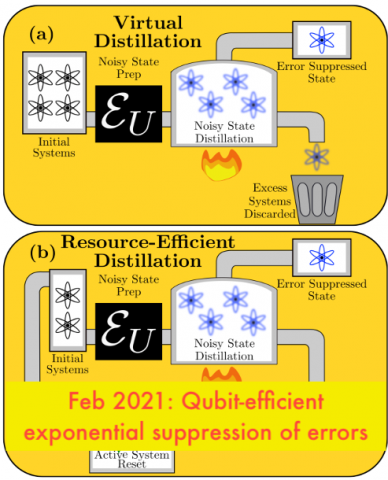
Qubit-efficient exponential suppression of errors
We propose a novel error mitigation method that exponentially suppresses errors with a fixed number of qubits. Our method is feasible for the quantum advantage regime. Error mitigation will be necessary for practical quantum advantage. Most error mitigation methods do not provide exponential suppression of errors. An exception is virtual distillation, but its large qubit…
-
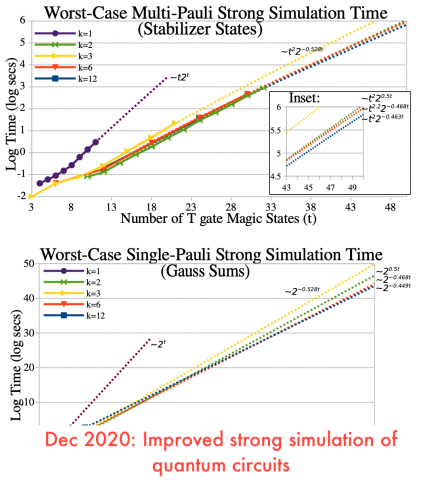
Improved strong simulation of qubit quantum circuits
Multi-Pauli measurements on magic states is one way to formulate universal quantum computing. We lower the asymptotic bound to 2∼0.463t for multi-Pauli measurements on t magic states, improving over the best previously found bound of 2∼0.468t. This not only improves our understanding of the difficulty of classically simulating quantum circuits, but also results in the most…
-
Prove-It: A Proof Assistant for Organizing and Verifying General Mathematical Knowledge
We introduce Prove-It, a Python-based general-purpose interactive theorem-proving assistant designed with the goal of making formal theorem proving as easy and natural as informal theorem proving. Prove-It uses a highly-flexible Jupyter notebook-based user interface that documents interactions and proof steps using LaTeX. Prove-It is a theorem-proving assistant that is designed with flexibility and expressivity in…