-
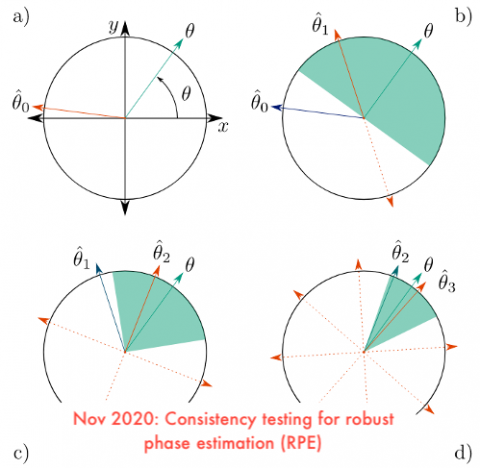
Consistency testing for robust phase estimation
The robustness of robust phase estimation (RPE) relies on noise being below a particular threshold. While it is difficult or impossible to directly test the violation of this threshold, we developed a set of consistency checks that herald whether there might be violations in a data set. We tested these checks for common noise models and identified…
-
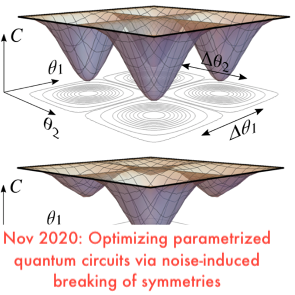
Optimizing parametrized quantum circuits via noise-induced breaking of symmetries
We analytical prove two results for parametrized quantum circuits (PQCs): (1) We find an exponentially large symmetry, which leads to an exponentially large degeneracy in the cost landscape minima. (2) We show that this degeneracy is broken by noise. We propose a novel optimizer called Symmetry-based minima hopping (SYMH), that exploits these results to enhance the…
-
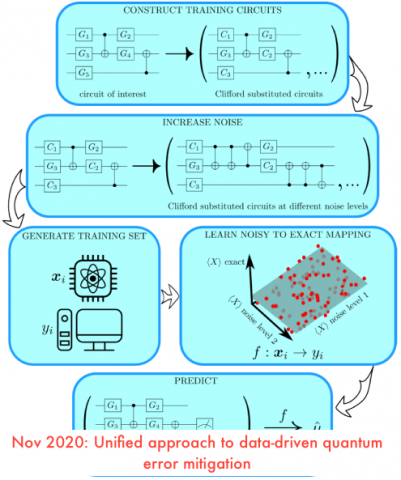
Unified approach to data-driven quantum error mitigation
Data-driven approaches to error mitigation are the current state-of-the-art. We unify two such approaches. One approach involves circuits with variable noise, and the other involves Clifford circuits. Our approach uses both types of data (Clifford circuits with variable noise), resulting in a method more powerful than the previous ones. Our method unifies zero-noise extrapolation (ZNE)…
-
DEIXIS article: A quantum bridge
“A quantum bridge”. Article in DEIXIS by Monte Bagsall on Department of Energy sponsored quantum information science research at Sandia, including a discussion of OVER-QC. Figure shows Sandia’s HOA 2 ion trap and is courtesy Susan Clark and the trapped ions group at Sandia.
-
Custom fermionic codes for quantum simulation
We present a fully customizable construction for designing quantum codes for systems of fermions on a quantum computer. The required number of qubits and the gate counts determine the feasibility of a quantum simulation experiment. The construction presented lets one realize a trade-off between these two resources and in some cases lower both costs simultaneously. This work…
-
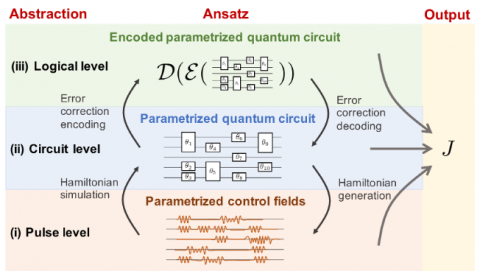
A quantum optimal control perspective on variational quantum algorithms
We provide an overview of variational quantum algorithms (VQAs) from the perspective of quantum optimal control (QOC). We integrate both fields in a common framework that enables identification of several QOC-inspired avenues for improving VQA performance on near-term quantum hardware. VQAs present some of the most promising applications of near-term quantum computing hardware. By connecting…
-
Quantum state verification in the quantum linear systems problem
We analyze the complexity of quantum state verification (QSV) in the context of solving systems of linear equations and provide complexity bounds that show that any verification procedure for this problem is “expensive”. Our results are an important contribution to quantum complexity and, among other implications, show that checking that the solution to a linear…