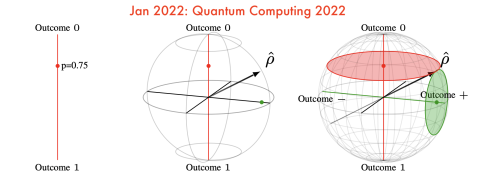
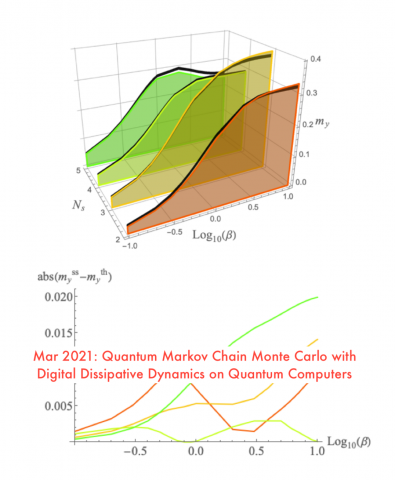
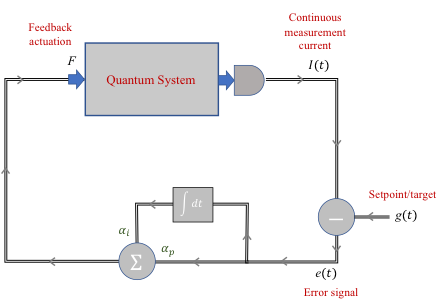
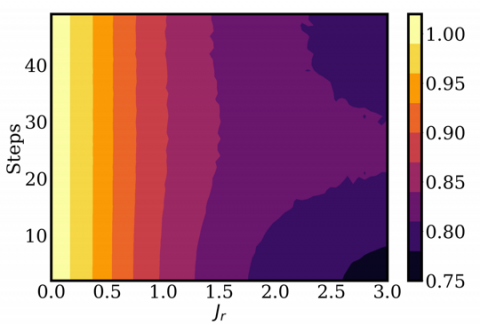
Post, February 25, 2021 • We introduce Prove-It, a Python-based general-purpose interactive theorem-proving assistant designed with the goal of making formal theorem proving as easy and natural as informal theorem proving. Prove-It uses a highly-flexible Jupyter notebook-based user interface that documents interactions and proof steps using LaTeX. Prove-It is a theorem-proving assistant that is designed...